A square or not a square?
One remarkable fact about school maths is that students are hardly ever given definitions of the objects they are dealing with. Instead, students are presented with some sort of descriptions. Here is an excerpt from BBC Bitesize which is a typical example of what school textbooks say:
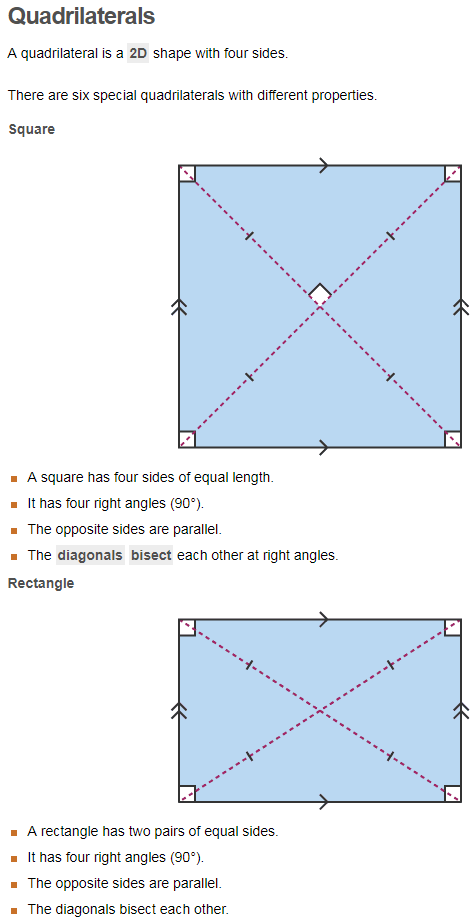
Students need to know properties of squares, but they are not told what kind of shape is called a square. If a quadrilateral has all four sides equal, does that mean that the quadrilateral is a square?
Also, the fact that a square is a special type of a rectangle is not mentioned. On the contrary, squares and rectangles are classified as different kinds of quadrilaterals, which muddles up the hierarchy of the quadrilaterals and leads to unnecessary repetition of properties.
One can scroll a bit further down the Bitesize page, but there is no improvement:
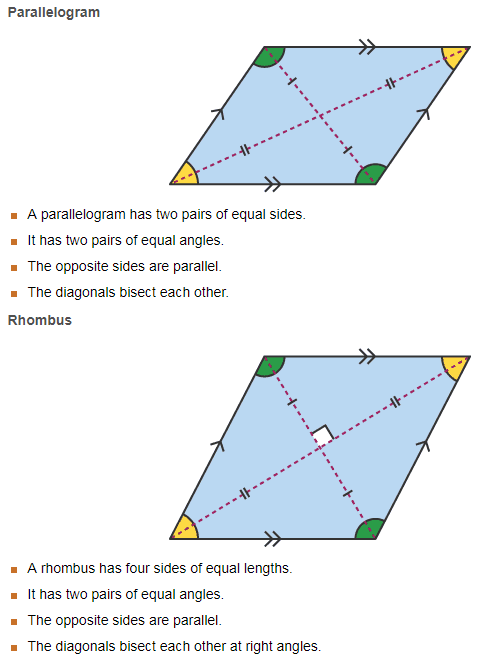
A rhombus is not recognised as a special case of a parallelogram, nor it is pointed out that parallelograms make up a wide class of quadrilaterals that includes rectangles as well.
It is not surprising that after being exposed to this poor attempt at classification, the students cannot distinguish between definitions, necessary conditions (properties), and sufficient conditions. Those are the basics of logical reasoning, the key ideas that make learning about shapes a worthwhile experience. If they are not explored, the whole topic of quadrilaterals becomes useless for development of mathematical abilities.
The mindless memorising of properties is also useless for practical purposes. Suppose you have a wooden board that looks like a square. How do you actually check whether it is a square or not? What would be the most efficient test of “squareness”—the list of properties does not answer this simple question.
The new curriculum, the government promised, will bring academic rigour to school subjects. However, the new textbooks are still written in the same vague manner and are full of obscure descriptions, superficial explanations, and mistakes of all kinds. The treatment of quadrilaterals one can see in recently published textbooks is broadly the same as on Bitesize. The opportunity to provide students with resources of the highest quality has been sadly wasted.