Unfit for learning
This is a chart called “100 square” that you can find in every primary clasroom:
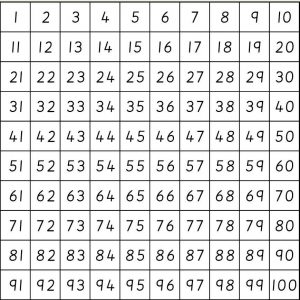
Children mostly use it for simple sums. Say, if you need to do 45+7, you find 45 on the chart and simply move 7 steps forward. Oops, sorry, you move only five steps forward, then you have to move your eye or your finger to the beginning of the next row –this will be your sixth step – and complete the task by making the last, seventh move. A bit awkward, but children are very flexible and never complain. One advantage is that if your sum is 45 +10, the task becomes really simple: you just move one row down. Don’t forget: if it’s units you are adding, you move right (well, sometimes you have to move left to the beginning of the next row as well). If you are adding tens, move down, and if it’s both units and tens, as in 45+17, you do both. Just remember the rule and please be careful: with so many numbers in your field of vision it’s easy to get confused.
Some questions still remain though. Where are the numbers greater than 100? Where are zero and negative numbers? Where are decimals? Let’s hope that by the time children start asking these questions, the 100 square will be long forgotten.
Yet in later years it gets dusted off and used again. Children then colour squares with multiples of 3 and admire the pattern. This could be a meaningful task if they were encouraged to think why multiples of 2 and 5 line up in columns, but multiples of 3 do not, but this discussion hardly ever happens, and colouring merely serves as an entertaining time filler.
It really is time to replace this ubiquitous but awkward chart with something more helpful: simple number line will do the job much better. Any number is represented by a point on a number line, and as children learn about new kinds of numbers, there is no need to change the model, just extend the line or change the scale.
Addition on a number line is no harder than on the 100 square, with a bonus of consistency: adding 7 to any number means moving 7 steps right, neither left nor down. Adding 10 or 100 can be presented as making a jump to the same place in the next ten or hundred.
An important advantage of the number line is that it is a fractal, with numbers following the same pattern on different scales: the sequence 1, 2, 3, 4, 5,… is similar to 10, 20, 30, 40, 50,.. as well as 0.1, 0.2, 0.3, 0.4, 0.5 … etc. The idea of zooming in to deal with small numbers and zooming out for large numbers is very simple yet extremely powerful, as it puts all the numbers together in an easy-to-use natural structure, in contrast with artificial and rigid arrangement of 100 numbers.